Different waveforms sound different.  A sine wave sounds different than a square wave, which sounds different than the waveform that comes out of an accordion.   All these waves have unique timbres because they have different harmonic content.

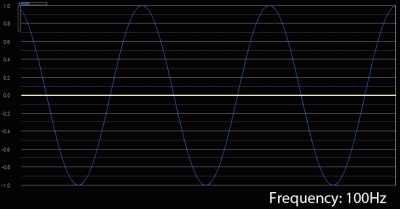
A harmonic is basically a multiple of a fundamental frequency.  For example, let’s say you’re playing a note with a frequency of 100Hz.  That would be the 1st harmonic.

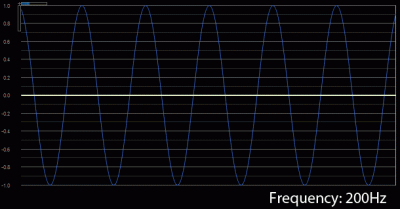
The 2nd harmonic would be twice that frequency, or 200Hz.

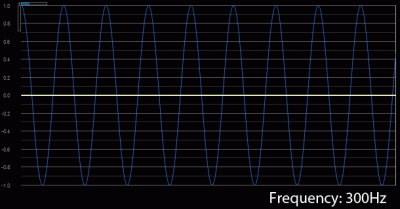
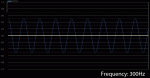
The 3rd harmonic would be 3  times the fundamental, or 300Hz.

You can see that it’s pretty easy to figure out the 4th, 5th 6th, etc.

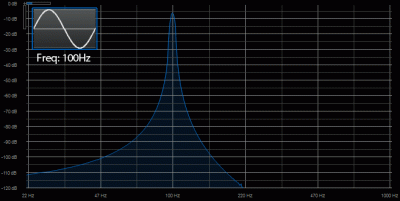
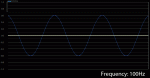
Now let’s do some frequency analysis of our different waveforms to see why they sound the way they do.  We’ll start with the sine wave:

In the spectrum analyzer display above, the horizontal axis (x) is frequency and the vertical axis (y) is level.  What it’s telling us is how much energy the signal has at various frequencies.  In the case of our sine wave, you can see that there is a single spike right at 100Hz.  That’s pretty much what we expect to see since it’s a 100Hz tone.

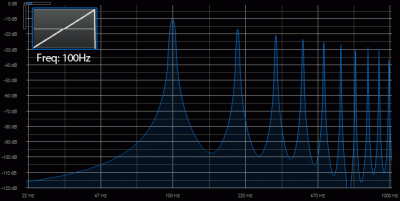
Now let’s look at a sawtooth:

Notice that the sawtooth not only gives us a spike at the fundamental frequency, there are also some smaller spikes at each harmonic frequency going up (200Hz, 300Hz, 400Hz, etc.)  The triangle wave contains the fundamental and a whole series of harmonics, which explains why it sounds so much different than a sine wave.

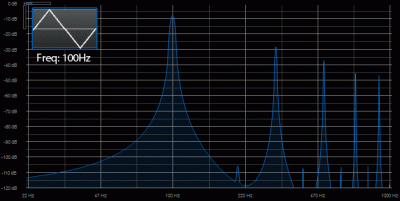
Now let’s check out a triangle wave:

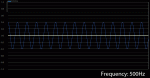
Once again we have several spikes, but this time they’re only at the odd-numbered harmonics (3rd=300Hz, 5th=500Hz, etc.).

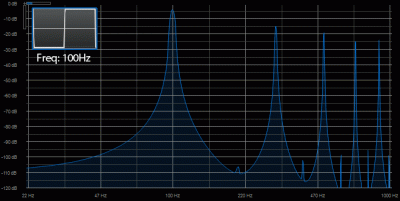
Here’s what a square wave looks like:

Like the triangle wave, the square wave contains odd harmonics, but they fall off less rapidly as the frequency increases.

Waveforms tend not to contain even harmonics if they are vertically symmetrical.  The square and triangle waves above are perfectly mirrored above and below the horizontal center line, so they don’t have any even harmonics.  The sawtooth, on the other hand, is lopsided and does contain even harmonics.  This rule of thumb applies to other waveforms too.

Why do different waveforms contain different frequencies, even though they’re basically just a single frequency?  Let’s explore that.  Remember our sine wave?  It only contained its fundamental frequency with no additional harmonics.  A sine wave is a pure tone and can be used as a basic building block to create other wave shapes.    You can get just about any waveform you want by adding a series of sine waves at the correct frequency, amplitude and phase.

Let’s mix 3 sine waves together, 1 fundamental and two odd harmonics with descending amplitude, and see what we get.  Note that when you mix (add) waves you end up with another single wave rather than what looks like two waves on top of each other.  This is because each wave is pushing or pulling on the same medium (your eardrum, the voltage in a wire, a digitally stored value; it doesn’t matter).  The values of each wave add at every point along the wave.  Adding two identical waves will give you a wave with the same frequency but twice the amplitude.  Two identical waves that are 180° out of phase (the positive peaks of one line up with the negative peaks of the other) will add to 0 at all points and cancel each other out.

Here are the source waves that we’ll be mixing (click to enlarge):

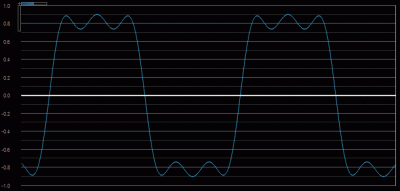
Here is what they look like mixed together (with some minor gain adjustments to prevent clipping):

Notice that they’re starting to resemble a square wave?  If we kept adding more and more sine waves at just the right frequencies, phases and amplitudes we would get closer and closer to a perfect square wave.

Waves don’t always have to have spikes at frequencies that are even multiples of the fundamental.  Sometimes they’re in-between or they appear seemingly at random.  These types of waves are considered to be inharmonic.  Because the spikes don’t fall at musical intervals, inharmonic waves can sound quite dissonant (like a cymbal).  Just a touch of inharmonicity can actually add “warmth” to a sound, as in the case of a piano.

We’ve been looking at some very basic waves which don’t often exist in nature.  The ability to generate these waves with a synthesizer means you can create a vast array of sounds that would be difficult to replicate without the use of electronics.  Acoustic instruments, on the other hand, tend to produce waves that are far more complex.  This is why it’s tough to create a patch that accurately mimics a piano, guitar or trumpet.